About this game
This game is a simple demonstration of MiniMax, which is an algorithm for finding the move which minimizes the opponent's best moves. This is a brief overview of the game's technical highlights.
Minimax with alpha-beta pruning
The Minimax algorithm represents every game as a tree of moves, with the current game position at the root of the tree. The algorithm is recursive with exponential time complexity and can have a very high branching factor: after the first move there are 225-1=224 possible moves. Because it is not feasible to evaluate all possible games to completion, Minimax calculation is usually limited to a fixed depth, after which the algorithm evaluates terminal leaf nodes using the gameover function and the static evaluator.
After each human move, Minimax assigns a score to each of the possible reply moves. By convention, the AI will score favorable moves with a positive score, and unfavorable moves with a negative score. The move corresponding to the highest score is then selected. In other words, the AI is called the "maximizer". Likewise, the human is known as the minimizer. To determine the score of each possible move, the minimax algorithm will recursively either maximize or minimize the possible moves available. After a given depth, the evaluation will stop, and return either an infinite value (+∞ for an AI win, -∞ for human win) or a finite evaluation of the state of the board. This static evaluation can be rather expensive, but luckily even a rough approximation is effective.
In practice, in addition to a depth limitation, this minimax algorithm also reduces the branching factor by limiting the squares which will be evaluated to those which are adjacent to squares which have been played. Given the fact that a disconnected "island" square cannot immediately lead to a win, this seems to be a reasonable simplification.
At the leaf nodes of the tree, either the game is over (the human has won or the computer has won) or the board needs to be evaluated with regards to who is winning.
Minimax with alpha-beta pruning
Alpha-beta pruning is an improvement on the minimax algorithm, reducing the number of branches and leaf nodes which need to be evaluated. This is acheived by "pruning" unnecessary branches, ignoring them because the parent minimizer/maximizer would never choose it. For a maximizer (whose parent is a minimizer), this will occur if the parent minimizer has already seen a lower evaluation than a number the maximizing child sees.Static evaluator
This function is used to evaluate a board position with regards to which player is winning, and by how much. The MiniMax algorithm will then choose the highest value for itself, while minimizing the options for its opponent. For gomoku, it was important to derive an evaluation function which could be calculated quickly, and which builds towards the final desired result of 5 squares in a row. Note that such a function would necessarily be isomorphic in four directions: vertical, horizontal, and on both diagonals.
My initial thought was that this would be extremely computationally expensive. There are many permutations of selected squares which can lead to a win, and many which do not. For example, XX--OOO--XX with O to move will lead to a win for O, but with X to move will not. However, I convinced myself that any static evaluation which built towards a win would find winning nodes at sufficient depth, so finding extremely detailed evaluation was less important than a general approximation.
Building from this thought, I decided to count the number of 4-in-a-rows (4s) and give them a high score, along with the 3s and 2s. Each in-a-row would be given an exponentially increasing "reward", so that 4s scores much higher than 2×2s. For example, the payout function might be f(n) = 2^N for 2, 3, and 4 so that f(4) = 16 and 2×f(2) = 8. This ensures the desired result, that the optimal configuration of N squares is Ns.
Eventually, I determined that it was sufficient to simply count 2s with overlaps, since allowing double counts would still favor longer strings of squares, but would not require separate checks for each length. Therefore, if 2s was rewarded 1, then XXX would be rewarded 2, and XXXX would be rewarded 3. This means that 4s is still more the most efficient configuration of four squares, since XX-XX only evaluates to 2.
Gameover function
This function simply needs to return true if the game is over and a player has won. After the simplifications to the static evaluator, the gameover function behaves almost identically. Instead of counting 2s, we check for the presence of 5s.
Bitmasks
Here is where the fun begins. I realized that a very efficient way of representing a game board was with a sequence of bits, where 1 represented an occupied square, and 0 represented an unoccupied square. A game state would therefore only require a bit sequence for each player (the game engine would prevent overlapping bits). For a 15×15=225 square board, each player's occupied squares could be represented with a number 225 bits in length. Although Javascript `Number`s are only 53 bits long, Javascript has a newer primative, `BigInt`, which can store numbers of arbitrary length.
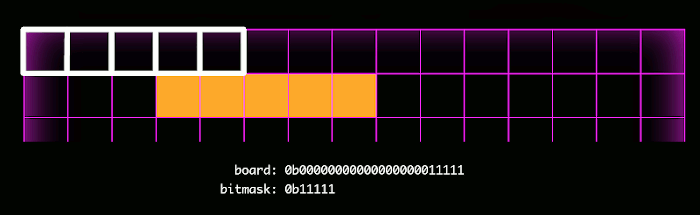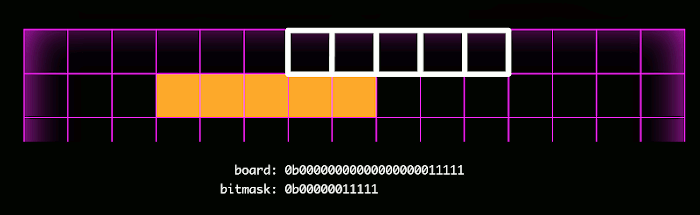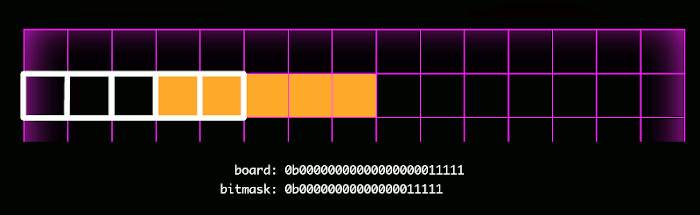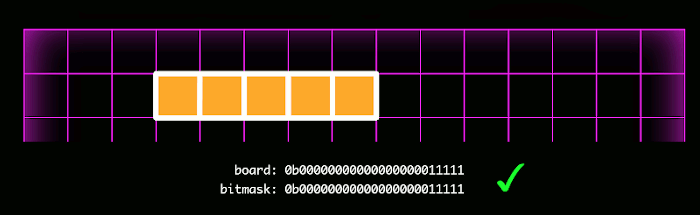
The biggest benefit of representing the game board this way is that it facilitates bitwise operations, which drastically reduces the time complexity for the static evaluator and gameover functions.
About BigInt
The BigInt primitive in Javascript is a newer built-in object, and as such is unsupported in some browsers. In particular, Internet Explorer and Safari do not have BigInt as a primitive. Although there are polyfills available for BigInt, I decided that as a demonstration of the Minimax algorithm, supporting all browsers was not my highest priority.